When working on sites with traffic, there is as much to lose as there is to gain from implementing SEO recommendations.
The downside risk of an SEO implementation gone wrong can be mitigated using machine learning models to pre-test search engine rank factors.
Pre-testing aside, split testing is the most reliable way to validate SEO theories before making the call to roll out the implementation sitewide or not.
We will go through the steps required on how you would use Python to test your SEO theories.
Choose Rank Positions
One of the challenges of testing SEO theories is the large sample sizes required to make the test conclusions statistically valid.
Split tests – popularized by Will Critchlow of SearchPilot – favor traffic-based metrics such as clicks, which is fine if your company is enterprise-level or has copious traffic.
If your site doesn’t have that envious luxury, then traffic as an outcome metric is likely to be a relatively rare event, which means your experiments will take too long to run and test.
Instead, consider rank positions. Quite often, for small- to mid-size companies looking to grow, their pages will often rank for target keywords that don’t yet rank high enough to get traffic.
Over the timeframe of your test, for each data point of time, for example day, week or month, there are likely to be multiple rank position data points for multiple keywords. In comparison to using a metric of traffic (which is likely to have much less data per page per date), which reduces the time period required to reach a minimum sample size if using rank position.
Thus, rank position is great for non-enterprise-sized clients looking to conduct SEO split tests who can attain insights much faster.
Google Search Console Is Your Friend
Deciding to use rank positions in Google makes using the data source a straightforward (and conveniently a low-cost) decision in Google Search Console (GSC), assuming it’s set up.
GSC is a good fit here because it has an API that allows you to extract thousands of data points over time and filter for URL strings.
While the data may not be the gospel truth, it will at least be consistent, which is good enough.
Filling In Missing Data
GSC only reports data for URLs that have pages, so you’ll need to create rows for dates and fill in the missing data.
The Python functions used would be a combination of merge() (think VLOOKUP function in Excel) used to add missing data rows per URL and filling the data you want to be inputed for those missing dates on those URLs.
For traffic metrics, that’ll be zero, whereas for rank positions, that’ll be either the median (if you’re going to assume the URL was ranking when no impressions were generated) or 100 (to assume it wasn’t ranking).
The code is given here.
Check The Distribution And Select Model
The distribution of any data represents its nature, in terms of where the most popular value (mode) for a given metric, say rank position (in our case the chosen metric) is for a given sample population.
The distribution will also tell us how close the rest of the data points are to the middle (mean or median), i.e., how spread out (or distributed) the rank positions are in the dataset.
This is critical as it will affect the choice of model when evaluating your SEO theory test.
Using Python, this can be done both visually and analytically; visually by executing this code:
ab_dist_box_plt = (
ggplot(ab_expanded.loc[ab_expanded['position'].between(1, 90)],
aes(x = 'position')) +
geom_histogram(alpha = 0.9, bins = 30, fill = "#b5de2b") +
geom_vline(xintercept=ab_expanded['position'].median(), color="red", alpha = 0.8, size=2) +
labs(y = '# Frequency \n', x = '\nGoogle Position') +
scale_y_continuous(labels=lambda x: ['{:,.0f}'.format(label) for label in x]) +
#coord_flip() +
theme_light() +
theme(legend_position = 'bottom',
axis_text_y =element_text(rotation=0, hjust=1, size = 12),
legend_title = element_blank()
)
)
ab_dist_box_plt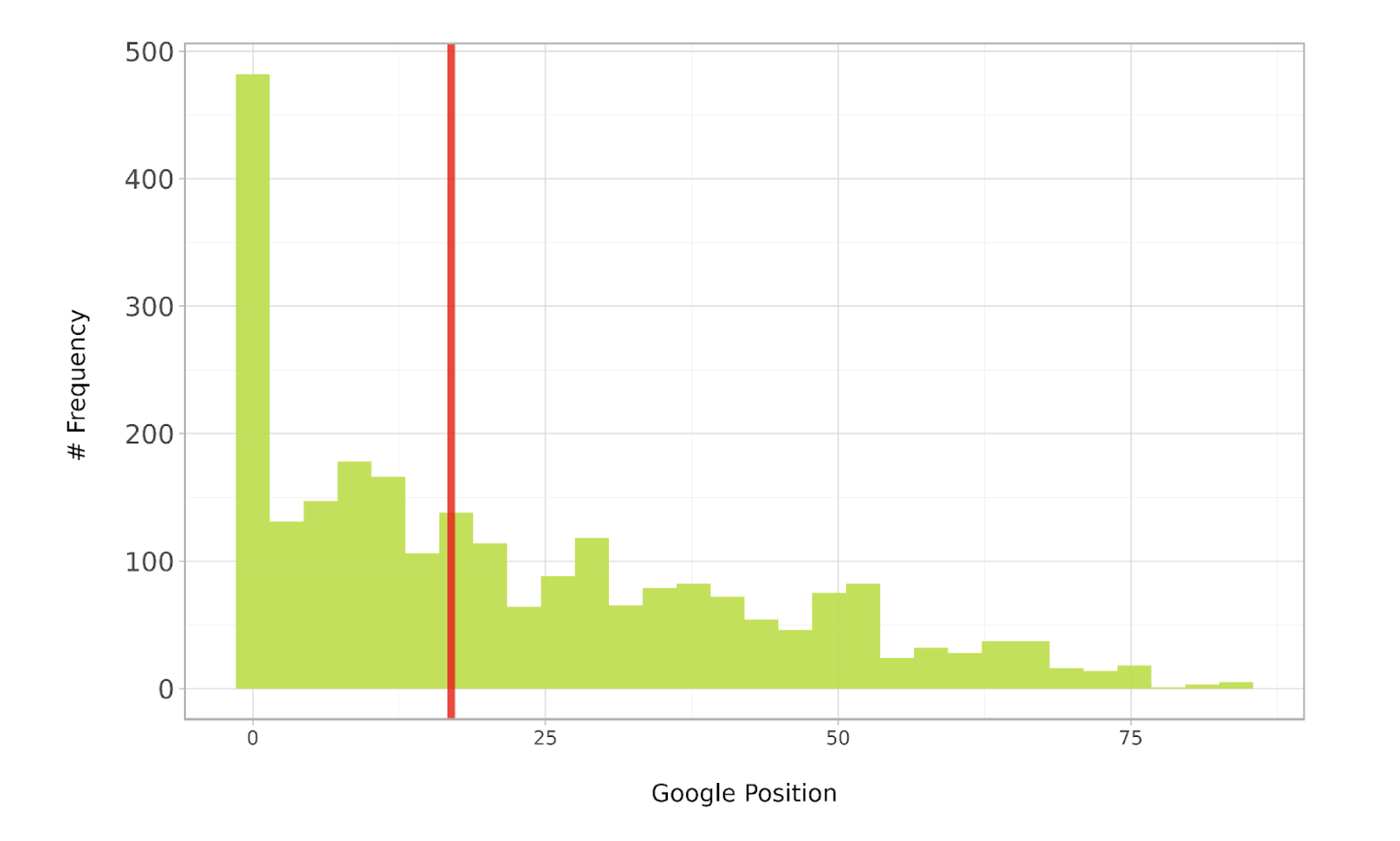
Image from author, July 2024The chart above shows that the distribution is positively skewed (think skewer pointing right), meaning most of the keywords rank in the higher-ranked positions (shown towards the left of the red median line).
Now, we know which test statistic to use to discern whether the SEO theory is worth pursuing. In this case, there is a selection of models appropriate for this type of distribution.
Minimum Sample Size
The selected model can also be used to determine the minimum sample size required.
The required minimum sample size ensures that any observed differences between groups (if any) are real and not random luck.
That is, the difference as a result of your SEO experiment or hypothesis is statistically significant, and the probability of the test correctly reporting the difference is high (known as power).
This would be achieved by simulating a number of random distributions fitting the above pattern for both test and control and taking tests.
The code is given here.
When running the code, we see the following:
(0.0, 0.05) 0
(9.667, 1.0) 10000
(17.0, 1.0) 20000
(23.0, 1.0) 30000
(28.333, 1.0) 40000
(38.0, 1.0) 50000
(39.333, 1.0) 60000
(41.667, 1.0) 70000
(54.333, 1.0) 80000
(51.333, 1.0) 90000
(59.667, 1.0) 100000
(63.0, 1.0) 110000
(68.333, 1.0) 120000
(72.333, 1.0) 130000
(76.333, 1.0) 140000
(79.667, 1.0) 150000
(81.667, 1.0) 160000
(82.667, 1.0) 170000
(85.333, 1.0) 180000
(91.0, 1.0) 190000
(88.667, 1.0) 200000
(90.0, 1.0) 210000
(90.0, 1.0) 220000
(92.0, 1.0) 230000To break it down, the numbers represent the following using the example below:
(39.333,: proportion of simulation runs or experiments in which significance will be reached, i.e., consistency of reaching significance and robustness.
1.0) : statistical power, the probability the test correctly rejects the null hypothesis, i.e., the experiment is designed in such a way that a difference will be correctly detected at this sample size level.
60000: sample size
The above is interesting and potentially confusing to non-statisticians. On the one hand, it suggests that we’ll need 230,000 data points (made of rank data points during a time period) to have a 92% chance of observing SEO experiments that reach statistical significance. Yet, on the other hand with 10,000 data points, we’ll reach statistical significance – so, what should we do?
Experience has taught me that you can reach significance prematurely, so you’ll want to aim for a sample size that’s likely to hold at least 90% of the time – 220,000 data points are what we’ll need.
This is a really important point because having trained a few enterprise SEO teams, all of them complained of conducting conclusive tests that didn’t produce the desired results when rolling out the winning test changes.
Hence, the above process will avoid all that heartache, wasted time, resources and injured credibility from not knowing the minimum sample size and stopping tests too early.
Assign And Implement
With that in mind, we can now start assigning URLs between test and control to test our SEO theory.
In Python, we’d use the np.where() function (think advanced IF function in Excel), where we have several options to partition our subjects, either on string URL pattern, content type, keywords in title, or other depending on the SEO theory you’re looking to validate.
Use the Python code given here.
Strictly speaking, you would run this to collect data going forward as part of a new experiment. But you could test your theory retrospectively, assuming that there were no other changes that could interact with the hypothesis and change the validity of the test.
Something to keep in mind, as that’s a bit of an assumption!
Test
Once the data has been collected, or you’re confident you have the historical data, then you’re ready to run the test.
In our rank position case, we will likely use a model like the Mann-Whitney test due to its distributive properties.
However, if you’re using another metric, such as clicks, which is poisson-distributed, for example, then you’ll need another statistical model entirely.
The code to run the test is given here.
Once run, you can print the output of the test results:
Mann-Whitney U Test Test Results
MWU Statistic: 6870.0
P-Value: 0.013576443923420183
Additional Summary Statistics:
Test Group: n=122, mean=5.87, std=2.37
Control Group: n=3340, mean=22.58, std=20.59The above is the output of an experiment I ran, which showed the impact of commercial landing pages with supporting blog guides internally linking to the former versus unsupported landing pages.
In this case, we showed that offer pages supported by content marketing enjoy a higher Google rank by 17 positions (22.58 – 5.87) on average. The difference is significant, too, at 98%!
However, we need more time to get more data – in this case, another 210,000 data points. As with the current sample size, we can only be sure that <10% of the time, the SEO theory is reproducible.
Split Testing Can Demonstrate Skills, Knowledge And Experience
In this article, we walked through the process of testing your SEO hypotheses, covering the thinking and data requirements to conduct a valid SEO test.
By now, you may come to appreciate there is much to unpack and consider when designing, running and evaluating SEO tests. My Data Science for SEO video course goes much deeper (with more code) on the science of SEO tests, including split A/A and split A/B.
As SEO professionals, we may take certain knowledge for granted, such as the impact content marketing has on SEO performance.
Clients, on the other hand, will often challenge our knowledge, so split test methods can be most handy in demonstrating your SEO skills, knowledge, and experience!
More resources:
Featured Image: UnderhilStudio/Shutterstock